right

乘法运算单元的设计

1. 两种常用的乘法算法
        1）Booth算法

        Booth算法主要用于补码的相乘。现将Booth归纳如下：
        ①符号位参加运算；
        ②在乘数最低位后面增加一位附加位（B-1），初值为0；
        ③部分积初值为0；
        ④ 每次以前一次部分积为基础，根据表7.2判断相邻两位之差（低位减高位）决定+[A]补、+[-A]补或不加；
        ⑤按补码规则右移一位；
        ⑥重复第4、第5步n次（n为数值的位数）；
        ⑦最后一次重复第4步，但不必移位。

        Booth算法的补码一位乘法又叫Radix-1+Booth算法。Radix-n+Booth算法是目前微处理器乘法运算单元中应用比较广的一种实现方法。

        2）累加算法
        乘法是在加法的基础上发展出来的一种计算方法，首先观察一下十进制的乘法的过程:

         在这个例子中，把1、0作为十进制数据进行计算，结果只有两种选择，每一次乘法操作如下：
        ①如果乘数位是1，将被乘数的拷贝放在恰当的位置。
        ②如果乘数位是0，将恰当的位置放0。
        我们可以仿造这一运算过程，设计自己的乘法算法，但以上只是最原始的累加过程，在设计乘法运算单元时可根据实际需要做改进。

2. 乘法运算单元的设计
        由于乘法运算单元需要同时支持无符号数和有符号数相乘，如果对于这两种乘法操作分别设计一个乘法运算单元来完成，在运算速度上会有优势，但会占用比较多的逻辑单元，增加实现成本。而且MiniSys SoC系统，对乘法运算单元速度上要求并不是很高，所以可以采用无符号数和有符号数乘法共用一个乘法运算单元的设计，既采用原码乘法，再单独处理符号位。
        我们可以使用累加算法加以一定的改进，来设计乘法运算单元，用原码来同时支持有符号数和无符号数的乘法。如果是原始累加算法，一个周期只判断一次乘数位，这样两个32位的数相乘就要32个周期计数，再加上前后两个符号调整周期，一共34个周期完成一次乘法操作，显然效率是很低的。结合硬件设计中高并行性的特点，可以对原始累加算法做必要的改进，利用如图7.7所示的四个周期来完成整个运算过程。

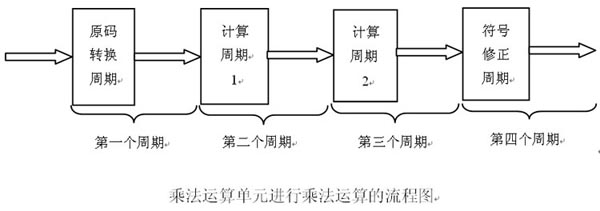
在第一个周期，对于补码表示的有符号数，要将补码转化为相应的原码。它必须在第二个周期之前就将数据准备好。进入第二周期，32个数据会分成6组分别进入六个加法阵列同时计算出累加结果。第三周期，再用一个加法阵列完成最终计算。第四周期，有符号数乘法要对结果进行符号修正，负数还要恢复成补码表示。乘积的符号实际上是被乘数和成熟的符号做异或运算的结果。
除法运算单元的具体实现请读者自己完成，欢迎到本网站论坛讨论区交流学习。